通信算法-Moose算法估计CFO

Intro

最近做通信的项目遇到了一个问题，在基带中还存在频偏，这种残余频偏被称之为载波频偏（Carrier Frequency Offset，CFO），基带信号处理时需要对CFO进行估计和补偿。

1994年P.H. Moose在其论文《A technique for orthogonal frequency division multiplexing frequency offset correction》1中提到过的算法是比较经典的CFO估计算法。 虽然该论文中讨论的调制方式是OFDM，但实际上该方法也适用于单载波通信的场景，其原理也非常简单，即用载波在两段相同的训练序列上的相位差来估计频偏。

CFO是接收端经过下变频之后存在的残余频偏，残余频偏来自于2个部分，其一是收发两段的LO本身存在频率差导致的，根源在于硬件时钟频率不可能严格相等，其二是由于收发双方有相对运动引入。

过程推导

Moose算法中提到了2段相同的训练序列，设定发送序列中包含两段相同的序列记为\(x[n]\)和\(x[n+L]\)，设相同序列部分的长度为\(N\)，如下图所示（均在数字域中处理）。

序列示意

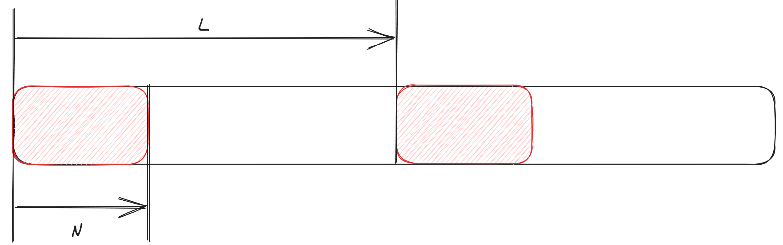
即满足 \[ x[n]=x[n+L], \forall n \in [0,N-1] \]

设信号经过高斯白噪声信道，经过收端下变频后存在残余频偏\(\Delta f\)，则接受信号可表示为：

\[ r(t) = s(t)\exp(j2\pi \Delta f t + \varphi) + n(t) \]

于是对于此处的两段序列而言可得: \[ \begin{aligned} r[n] &= x[n] \exp(j2\pi\Delta f n + \varphi) + n[n] \\ r[n+L] & =x[n+L] \exp\left(j2\pi\Delta f (n+L) + \varphi\right) + n[n+L] \end{aligned} \]

这里参考一下,2中写了详细推导，最终结果为： \[ \hat{\Delta f} = \frac{f_{smp}}{2\pi L}\cdot Arg\left\{ \sum_{n=0}^{N-1}r^*[n]r[n+L] \right\} \] 原始论文中采用的是MLE准则来估计参数，此处可以采用一个更简单的办法，即直接求期望，至于这种方法的正确性有待考证，只是一个思路。 若使用期望来进行求解，则有： \[ \begin{aligned} \mathbb{E}\left[r^*[n]r[n+L]\right]=& \mathbb{E}\Big[ \left\{ x[n] e^{j(2\pi\Delta f n + \varphi)} +n[n]\right\}^* \left\{ x[n+L] e^{j(2\pi\Delta f (n+L) + \varphi)} + n[n+L] \right\}\Big] \\ =&\mathbb{E}\left[ x[n]^*x[n+L]e^{j(2\pi \Delta fL)}\right] + \mathbb{E}\{\dots\} \end{aligned} \] 上式中除了第一项外，其他均含有噪声分量，此处考虑噪声分量为0均值高斯白噪声，自相关函数为狄拉克函数\(\delta(t)\)，而由于发送的是两段相同的序列，因此有： \[ \begin{aligned} \mathbb{E}\left[r^*[n]r[n+L]\right] &= \mathbb{E}\left[ x[n]^*x[n+L]e^{j(2\pi \Delta fL)}\right] \\ &=\left\|x[n]\right\|^2e^{j2\pi\Delta fL} \end{aligned} \] 于是可得: \[ \begin{aligned} 2\pi\Delta f L &= Arg\{\mathbb{E}\left[r^*[n]r[n+L]\right]\} \\\\ \Delta f &= \frac{Arg\{\mathbb{E}\left[r^*[n]r[n+L]\right]\}}{2\pi L} \\\\ \hat{\Delta f} &=\frac{Arg\left\{ \sum_{n=0}^{N-1}r^*[n]r[n+L] \right\}}{2\pi L} \end{aligned} \]

上式中利用了求均值来求期望的过程，这个是本推导中不严谨的一步。仔细分析上式，其本质是求相同序列经过L个采样点后相位的偏差，即CFO在经过\(L\)采样点时间后，在后一个采样点上积累了相位差，上式即是将这种相位差值求取期望，得到估计值（这里需要提出前提假设，CFO恒定不变）。

Moose算法的原论文是利用MLE推导求得估计值，文章3中利用的是最小二乘法求得估计值，此处我利用期望求得估计，（本质上应该是一样，但是不会推数学公式了）。 这里的\(\Delta f\)是数字归一化频率，范围是\([0,1]\)，由于辐角范围为\((-\pi,\pi]\)，因此可得Moose方法所能估计的CFO最大范围为：

\[ \left|\hat{\Delta f}\right| \le \frac{1}{2\pi L} \cdot \pi = \frac{1}{2L} \] \(L\)为两段相同序列的间隔，\(L\)越大，CFO最大估计范围越小，精度也越高。此外，相同序列点数长度\(N\)影响了估计中对噪声的影响，长度\(N\)越长，噪声对估计结果的影响越小，估计误差越小。

Simulation

以QPSK信号为例子（实际上两段训练序列不需要关注具体是什么信号，只需要两段序列相同即可）。 matlab仿真代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
clc;clear;close all;

N = 102400; % points of trainning seq
L = 204800; % interval sample points between two seqs' head, must be greater than N
fs = 50e6;
INTERPOLATION_RATE = 4;
MAX_FREQ_DEVIATION = 1/(2*L*INTERPOLATION_RATE);
alpha = 0.15;
EbN0 = 2;
hrc = rcosdesign(alpha,6,INTERPOLATION_RATE,"sqrt");
qpskmod = @(N) pskmod(randi([0 3],1,N),4);
fprintf("max CFO  :% 7.2E , max CFO fs % 7.4EHz\n",MAX_FREQ_DEVIATION,MAX_FREQ_DEVIATION * fs);

%% tx
tranning_seq = qpskmod(N); % this can use any seq in fact
data = [tranning_seq qpskmod(L-N) tranning_seq];
sBB = conv(upsample(data,INTERPOLATION_RATE),hrc);

%% channel
df = (2*rand-1)*MAX_FREQ_DEVIATION;
sBB_df = sBB.*exp(1j*(2*pi*df*(0:length(sBB)-1) + 2*pi*rand ));
% sBB_multipath = Multipath(sBB_df,INTERPOLATION_RATE);
sBB_multipath = sBB_df;
snr = EbN0 + 10*log10(2) - 10*log10(INTERPOLATION_RATE);
rBB = awgn(sBB_multipath,snr,"measured");

%% recv
rBB_mf = conv(rBB,hrc);%% match filter

%% moose algorithm
% remove some symbol to avoid the convolution's tail
offset = 32*INTERPOLATION_RATE;
ob1 = rBB_mf(1+offset:N*INTERPOLATION_RATE);
ob2 = rBB_mf(1+offset+L*INTERPOLATION_RATE:(N+L)*INTERPOLATION_RATE);

res = ob2.*conj(ob1);
res_mean = mean(res);
df_hat = angle(res_mean)/(2*pi*L*INTERPOLATION_RATE);
% analysis
err = (df_hat - df);
err_r = abs((df_hat - df)/df);
fprintf("hat df   :% 7.3E \tdf   : % 7.3E \n",df_hat,df);
fprintf("err a    :% 7.3E \terr r: % 7.3E\n",err,err_r);
fprintf("hat df fs:% 7.3fHz \tdf fs: % 7.3fHz \terr a fs:% 7.3fHz\n",df_hat*fs,df*fs,err*fs);


scr_siz = get(0,'ScreenSize');
f = figure();
f.Position = [scr_siz(3)/2 scr_siz(4)/2 0 0] + 800*[-0.5 -0.5 1 1];
scatter(real(res),imag(res),'b.','linewidth',0.2,'DisplayName','differential points');
hold on;
esti = linspace(0,max(abs(res)).*exp(1j*angle(res_mean)));
scatter(real(esti),imag(esti),'ro','DisplayName','frequency estimation');
axis(max(abs(res))*[-1 1 -1 1]);
ax = gca();
ax.XAxisLocation = "origin";
ax.YAxisLocation = "origin";
ax.Box = "on";
ax.Position = [0.05 0.05 0.9 0.9];
grid on;
legend();

仿真结果如下： 

1
2
3
4
max CFO  : 6.10E-07 , max CFO fs  3.0518E+01Hz
hat df   :-1.994E-07    df   : -1.989E-07 
err a    :-4.295E-10    err r:  2.159E-03
hat df fs: -9.968Hz     df fs:  -9.947Hz        err a fs: -0.021Hz

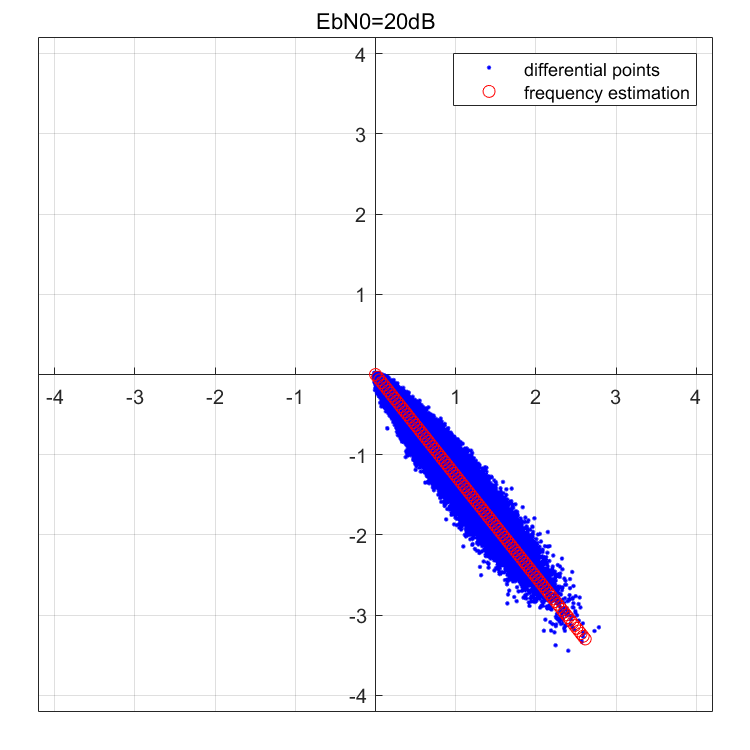
MATLAB仿真结果 高信噪比
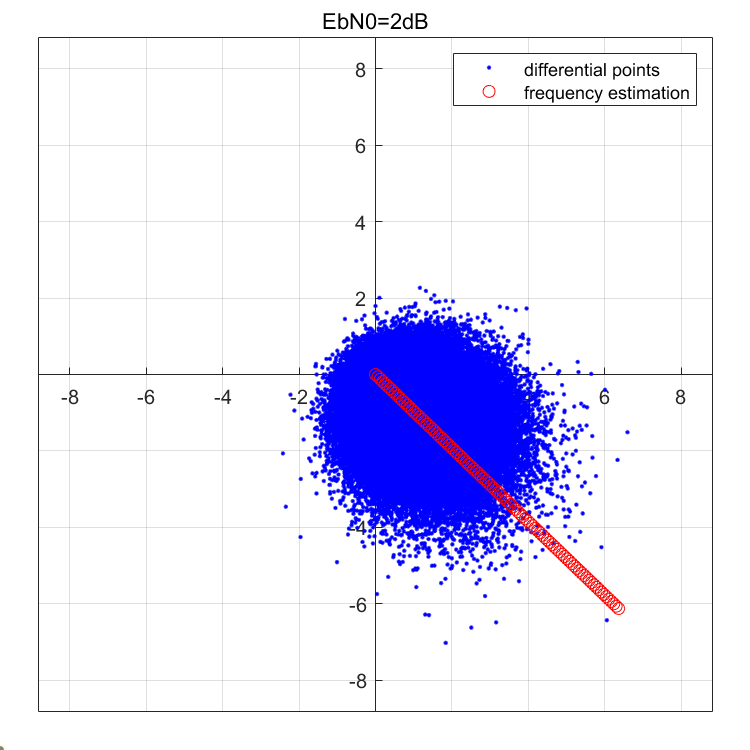
MATLAB仿真结果 低信噪比

可以看出低信噪比下相对误差仍然在\(10^{-3}\)这个量级，换算到50MHz的采样率下，经过纠正后的残余频偏几乎不剩多少，其估计效果还是很不错的。

Notice

卷积拖尾的影响

MATLAB代码中，有一个细节不能忽略，即 

1
2
% remove some symbol to avoid the convolution's tail
offset = 32*INTERPOLATION_RATE;
这里移除了前32个符号，因为实际发射机进行成型滤波后，前一个符号的波形会影响到后续，那么在这两段波形的最开始一定会收到其前面数据成型滤波拖尾的影响，这是因为Moose算法是在采样点级别做的。若不去掉该部分，则会影响最终估计准确性。

硬件实现精度

这里只给出了频偏估计范围（\(\frac{1}{2L}\)），从数学上看，若实际收端CFO落入到了该区间内，则一定能准确得到CFO的估计值，但在硬件实现的时候，受限于量化精度问题，verilog代码实现时会存在最小精度误差。

Reference

  1. A technique for orthogonal frequency division multiplexing frequency offset correction↩︎

  2. OFDM同步基础(一)|知乎专栏↩︎

  3. OFDM同步基础(一)|知乎专栏↩︎

通信算法
#载波同步 #算法
通信算法-Moose算法估计CFO
https://blog.zorogh.top/2024/04/20/通信算法-Moose算法估计CFO/
作者
ZoroGH
发布于
2024年4月20日
更新于
2024年4月21日
许可协议