超前进位加法器

简单记录一下超前进位加法器（Lookahead carrier adder），这里就不讲解行波进位了。

超前进位加法器的本质，就是把前级的加法结果全部获取到后直接计算出当前位的加法结果以及进位，为了方便Coding，假设下标从0开始，输入信号为Nbit向量A与B以及进位输入Ci，输出Nbit向量S和进位输出Co。

首先产生进位传递项P和进位产生项G，这其实是半加器的结果： \[ \begin{align} P_i&=A_i\oplus B_i&, 0\le i \le N-1 \\ G_i&=A_i B_i & , 0\le i \le N-1 \end{align} \] 然后就是根据P和G来产生S和进位输出Co \[ \begin{align} S_i &= P_i\oplus C_{i-1} \\ C_i &= G_i + P_iC_{i-1} \end{align} \] 需要注意的是，这里的\(C_{-1}\)即为输入的信号Ci，而最终的Co，应该是\(C_{N-1}\)，在Coding的时候，这个进位会多一位，可以把\(S_i\)的生成表达式中\(C_{i-1}\)替换为\(C'_{i}=C_{i-1}\)，这样描述起来更加方便。上面这个式子本质上来看没有完成超前进位的功能，仅仅是描述了递推关系式，这个其实还是一个行波进位，但就是因为存在这个超前进位的递推式子，从而可以将\(C_i\)展开为\(P\)和\(G\)的组合逻辑，比如\(C_2\)描述如下：

本人在这里犯了一个错误

\[ C_2 = G_2+P_2(G_1 + P_1C_{-1}) \] 可以发现通过递推关系，将进位项都分解为P和G的组合逻辑，那么延迟就变成了1级组合逻辑了，由于P和G的产生不依赖前级进位，只是简单的半加器，因此延迟低，而递推又解决了前级进位依赖的问题，从而用面积换取了延迟。

错误写法

对于一个4bit的超前进位加法器，verilog代码实现如下。

module lca_4bit (
    input       [3:0] A,
    input       [3:0] B,
    input             Ci,
    output wire [3:0] S,
    output wire       Co
);
	
    // generate p and g
    wire [3:0] p;
    wire [3:0] g;
    wire [4:0] c;

    assign p    = A ^ B;
    assign g    = A & B;

    // c, in fact c'_i = c_{i-1}
    assign c[0] = Ci;
    assign c[1] = g[0] | (p[0] & (c[0]));
    assign c[2] = g[1] | (p[1] & (g[0] | (p[0] & (c[0]))));
    assign c[3] = g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & (c[0]))))));
    assign c[4] = g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & (c[0]))))))));
    assign Co   = c[4];

    assign S    = p ^ c[3:0];

endmodule

仿真电路图如下所示：

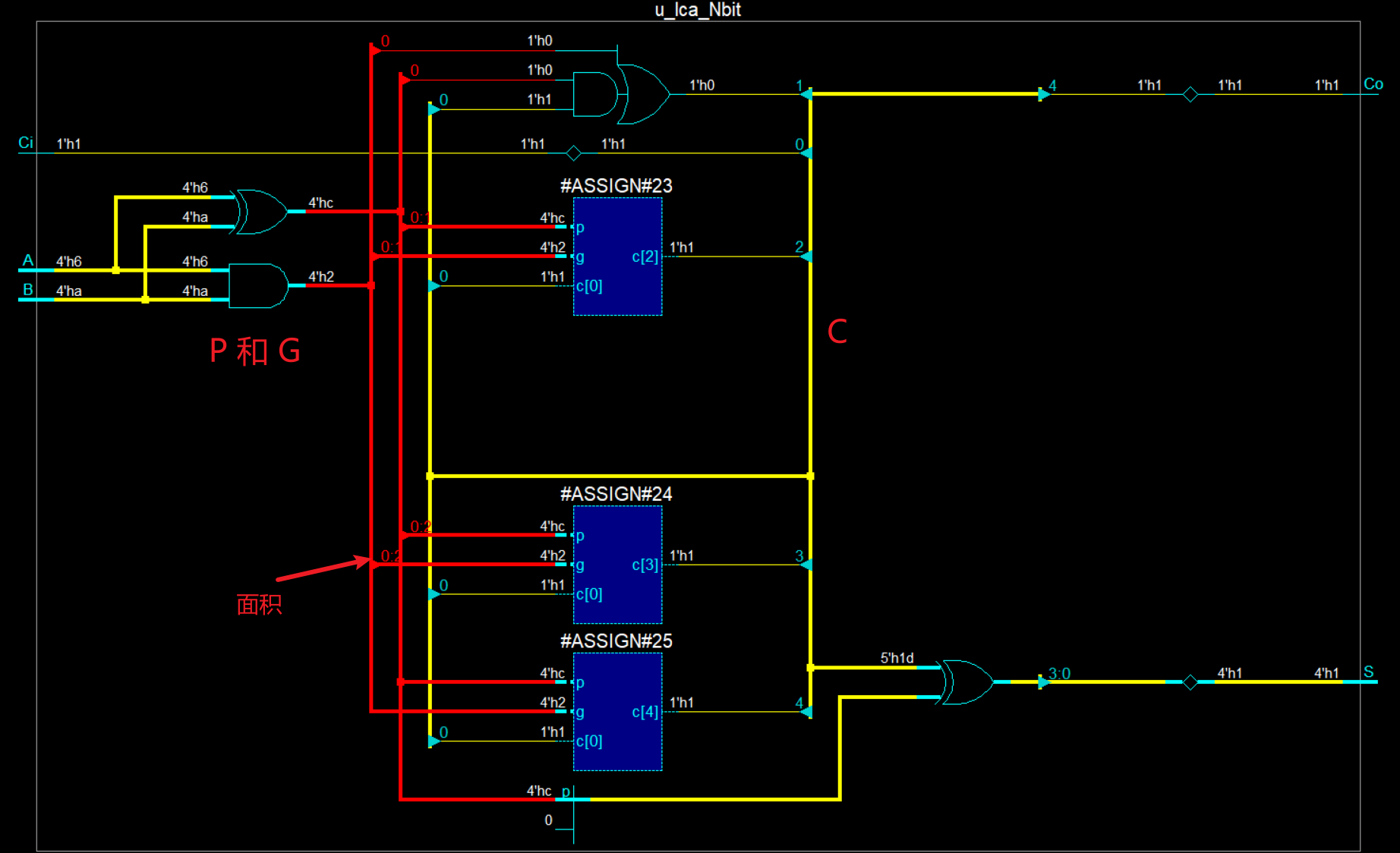
展开后得到如下结果，会发现信号传播路径依然很长，这就表明了这仍然是一个行波进位，回到上面的表达式里面来，可以发现我只是带入了相关的表达式，但是并没有进行展开，这就是问题所在，也就意味着，后一级的进位仍然依赖于前一级的进位信号。

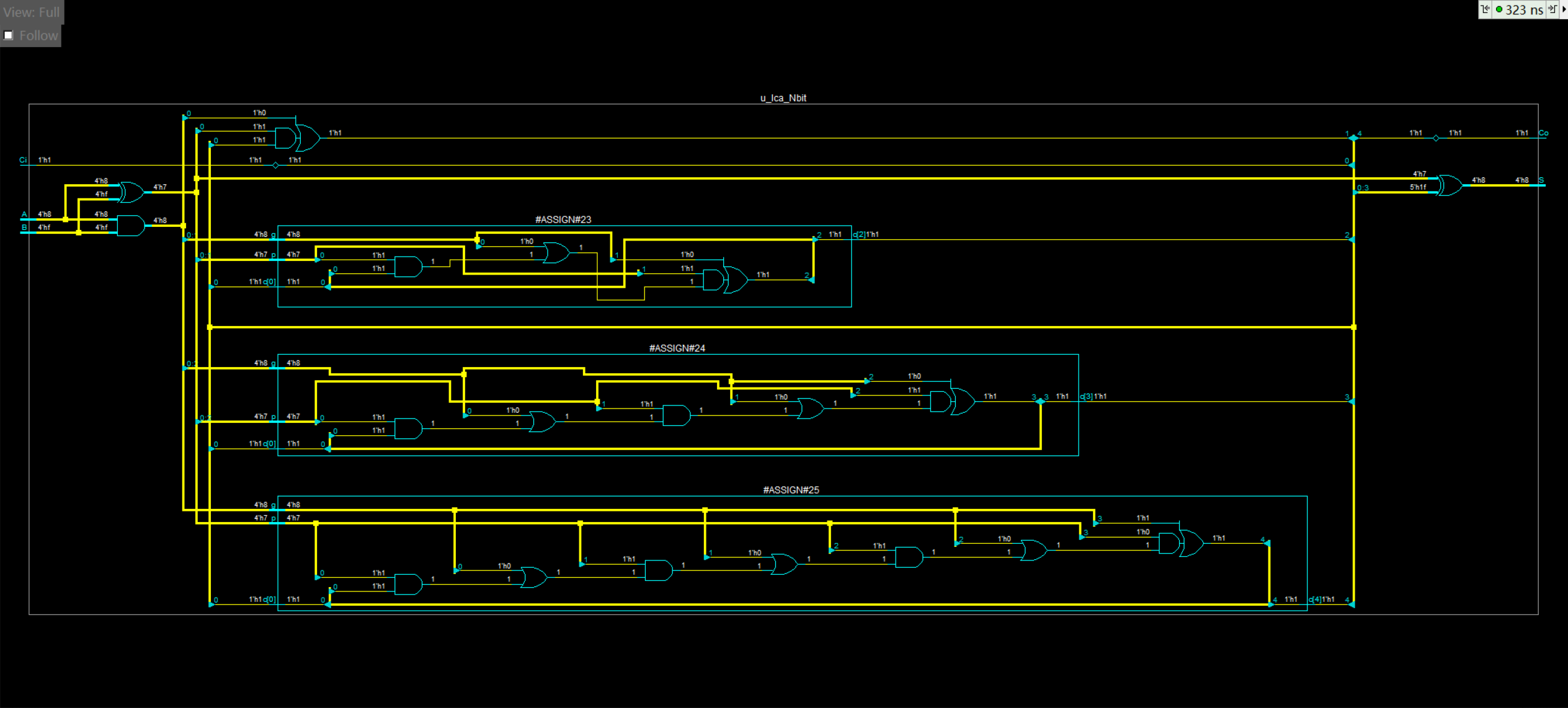
正确写法

所以在对于表达式进行处理的时候，要完全展开才可以，参考刚才计算C2的例子：

\[ C_2 = G_2+P_2(G_1 + P_1C_{-1})= G_2+ P_2G_1+P_2P_1C_{-1} \]

相当于必须要展开到P和G的与或形式才算完成了超前进位。

更新后的代码如下：

module lca_4bit (
    input       [3:0] A,
    input       [3:0] B,
    input             Ci,
    output wire [3:0] S,
    output wire       Co
);

    // generate p and g
    wire [3:0] p;
    wire [3:0] g;
    wire [4:0] c;

    assign p    = A ^ B;
    assign g    = A & B;

    // c, in fact c'_i = c_{i-1}
    assign c[0] = Ci;
    assign c[1] = g[0] | p[0] & Ci;
    assign c[2] = g[1] | p[1] & g[0] | p[1] & p[0] & Ci;
    assign c[3] = g[2] | p[2] & g[1] | p[2] & p[1] & g[0] | p[2] & p[1] & p[0] & Ci;
    assign c[4] = g[3] | p[3] & g[2] | p[3] & p[2] & g[1] | p[3] & p[2] & p[1] & g[0] | p[3] & p[2] & p[1] & p[0] & Ci;
    assign Co   = c[4];

    assign S    = p ^ c[N-1:0];

endmodule

仿真电路图如下：

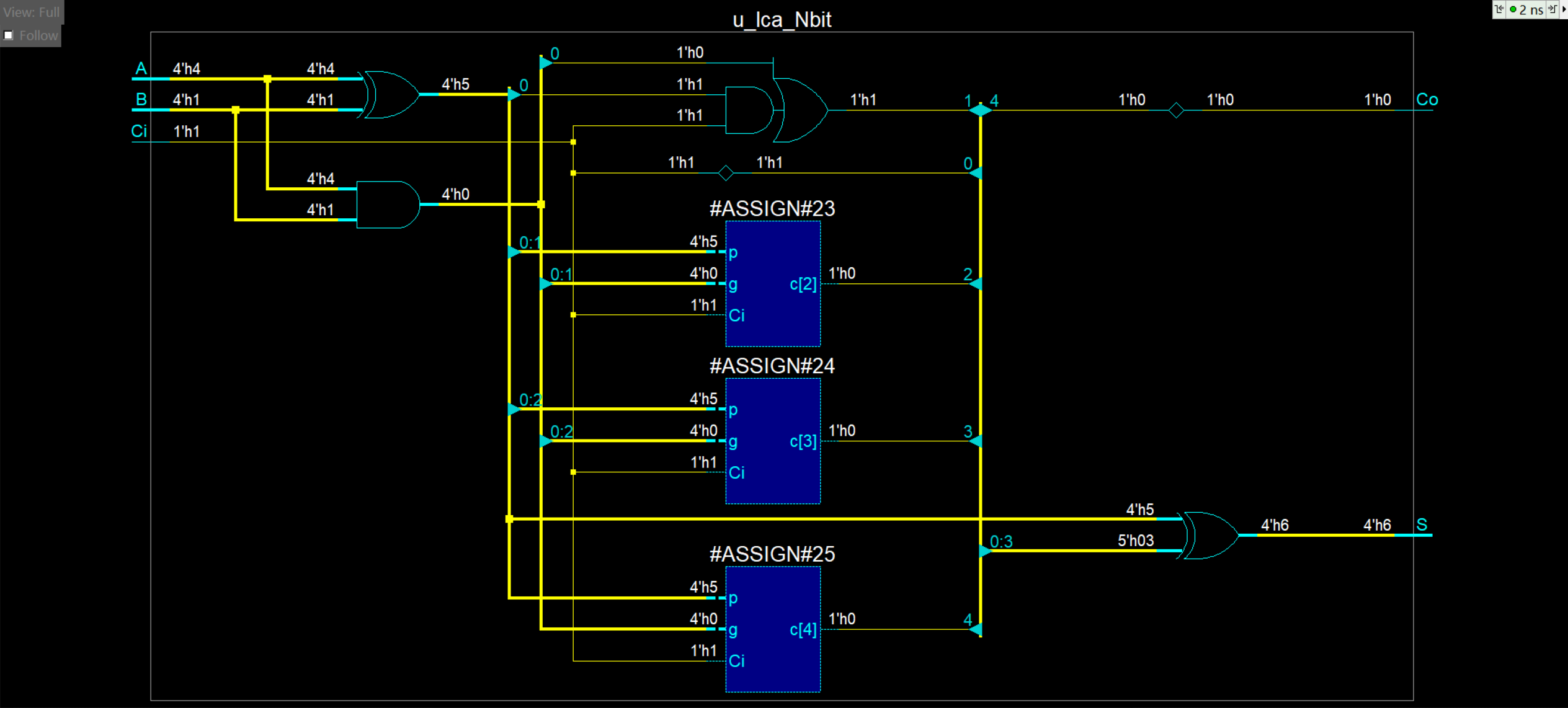
展开得到

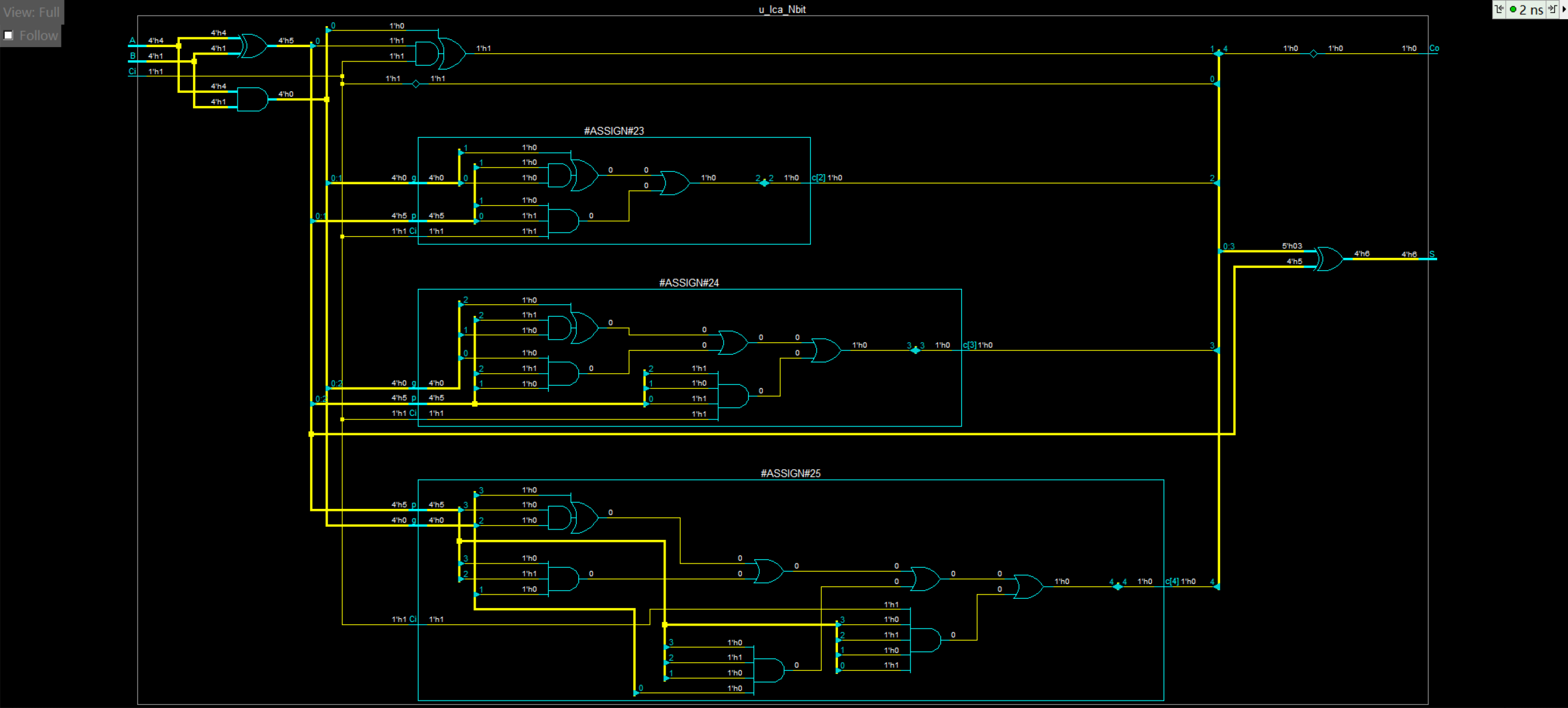
这里其实发现modelsim综合时没有用到多输入的或门，反倒是能用到多输入的与门，这个问题还需要进一步的研究。